1.1.3.2.3 Understanding Phase Difference through Uniform Circular Motion

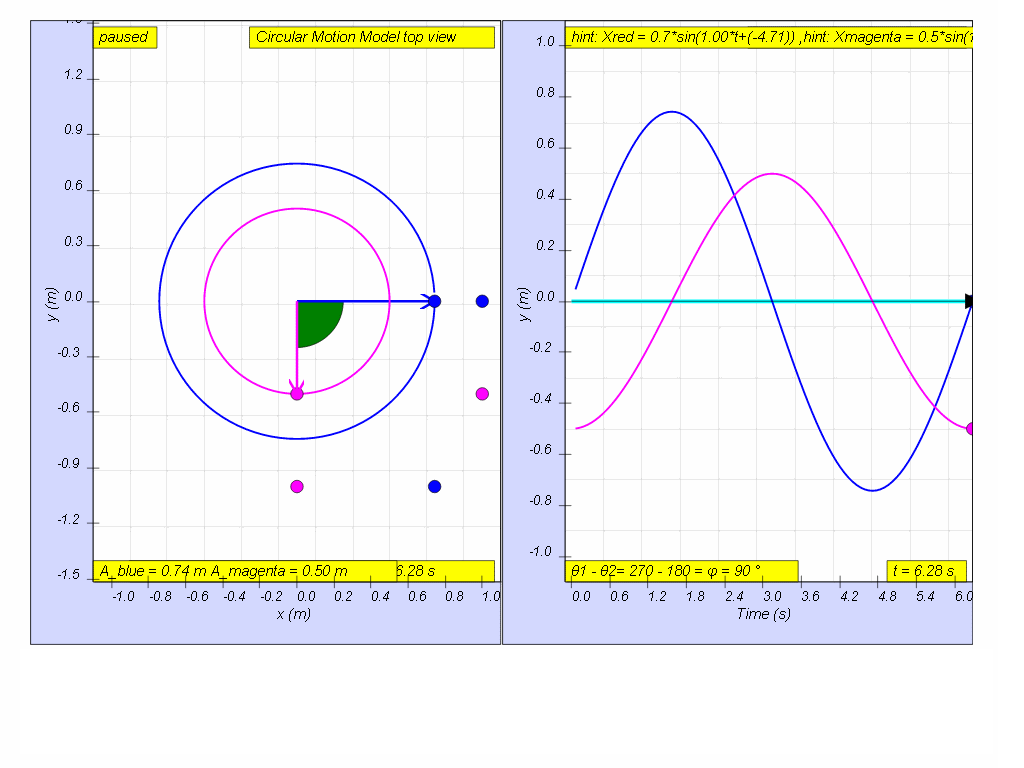
Simple harmonic motion can in some cases be considered to be the one-dimensional projection of uniform circular motion. If an object moves with angular speed ω around a circle of radius A centered at the origin of the x−y plane, then its motion along each coordinate is simple harmonic motion with amplitude A and angular frequency ω.

Q1: given that, a circular motion can be described by x = A cos(ω t)  and y A sin(ω t) what is the y-component model-equation that can describe the motion of a uniform circular motion?

A1: y = Asin (ωt)

Q2: When the x-component of the circular motion is modelled by x = A cos(ω t)  and y A sin(ω t) suggest an model-equation for y.

A2: y = Acos (ωt) for top position or y = - Acos (ωt) for bottom position

Q3: Explain why are the models for both x and y projection of a uniform circular motion, a simple harmonic motion?

A3: both x = A cos(ω t)  and y A sin(ω t) each follow the defining relationship for SHM as ordinary differential equations of   ${\displaystyle \frac{d^{2}x}{{dt}^2}=-{\omega }^{2}x}$ and  ${\displaystyle \frac{d^{2}y}{{dt}^2}=-{\omega }^{2}y}$ respectively.

Q4: In, the diagram above, what is the phase difference between blue and magenta color y direction motion?

1.1.3.2.3.1 YouTube:

http://youtu.be/0IaKcqRw_Ts This video shows how a pendulum's oscillations and the shadow of rotating object are related. This could be used to demonstrate that the projection of a circular motion is actually a simple harmonic motion.

1.1.3.2.3.2 Run Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/89