Solución

Usando la estrategia de resolución de problemas, el paso 1 implica encontrar los puntos críticos de $f$ en su dominio. Por lo tanto, primero calculamos $f_x (x, y)$ y $f_y (x, y)$, luego los igualamos a cero:
$$f_x(x, y) = 2x − 2y − 4$$ $$f_y(x, y) = −2x + 8y − 2$$ Igualamos a cero las ecuaciones:
$$\begin{aligned} 2x − 2y − 4 &= 0\\ −2x + 8y − 2 &= 0 \end{aligned}$$ La solución a este sistema es $x = 3$ e $y = 1$. Por lo tanto $(3, 1)$ es un punto crítico de $f$. Al calcular $f (3, 1)$ obtenemos $f (3, 1) = 17$.

El siguiente paso consiste en encontrar los extremos de $f$ en el límite de su dominio. El límite de su dominio consta de cuatro segmentos de línea como se muestra en el siguiente gráfico:

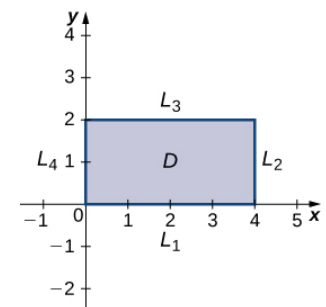
Figura 4.52. Gráfica de la función $f(x, y) = x^2 − 2xy + 4y^2 − 4x − 2y + 24$

$L_1$ es el segmento de línea que conecta $(0, 0)$ y $(4, 0)$, y se puede parametrizar mediante las ecuaciones $x (t) = t, y (t) = 0$ para $0 \le t \le 4$. Definamos $g (t) = f \big(x (t), y (t)\big)$. Esto da $g (t) = t^2 - 4t + 24$. La diferenciación de $g$ lleva a $g ^{\prime}(t) = 2t - 4$. Por lo tanto, $g$ tiene un valor crítico en $t = 2$, que corresponde al punto $(2, 0)$. Al calcular $f (2, 0)$ da el valor $z = 20$.

$L_2$ es el segmento de línea que conecta $(4, 0)$ y $(4, 2)$, y se puede parametrizar mediante las ecuaciones $x (t) = 4, y (t) = t$ para $0 \le t \le 2$. Nuevamente, definamos $g (t) = f \big(x (t), y (t)\big)$. Esto da $g (t) = 4t^2 - 10t + 24$. Entonces, $g ^{\prime}(t) = 8t - 10$. g tiene un valor crítico en $t = \frac54$, que corresponde al punto $\big(0, \frac54\big)$.

Al calcular $f \big(0,\frac54\big)$ da el valor $z = 27,75$

$L_3$ es el segmento de línea que conecta $(0, 2)$ y $(4, 2)$, y se puede parametrizar mediante las ecuaciones $x (t) = t, y (t) = 2 $para $0 \le t \le 4$. Nuevamente, definamos $g (t) = f \big(x (t), y (t)\big)$. Esto da $g (t) = t^2 - 8t + 36$.
El valor crítico corresponde al punto $(4, 2)$. Entonces, al calcular $f (4, 2)$ da el valor $z = 20$.

$L_4$ es el segmento de línea que conecta $(0, 0)$ y $(0, 2)$, y se puede parametrizar mediante las ecuaciones $x (t) = 0, y (t) = t$ para $0 \le t \le 2$. Esta vez, $g (t) = 4t^2 - 2t + 24$ y el valor crítico $t = \frac14$ corresponde al punto $\big(0, \frac14\big)$. Al calcular $f \big(0, \frac14\big)$ da el valor $z =23.75$.

También necesitamos encontrar los valores de $f (x, y)$ en las esquinas de su dominio. Estas esquinas se encuentran en $(0, 0), (4, 0), (4, 2)$ y $(0, 2)$:
$$\begin{aligned} f(0, 0) &= (0)^2 − 2(0)(0) + 4(0)^2 − 4(0) − 2(0) + 24 = 24\\ f(4, 0) &= (4)^2 − 2(4)(0) + 4(0)^2 − 4(4) − 2(0) + 24 = 24\\ f(4, 2) &= (4)^2 − 2(4)(2) + 4(2)^2 − 4(4) − 2(2) + 24 = 20\\ f(0, 2) &= (0)^2 − 2(0)(2) + 4(2)^2 − 4(0) − 2(2) + 24 = 36 \end{aligned}$$ El valor máximo absoluto es $36$, que ocurre en $(0, 2)$, y el valor mínimo global es $20$, que ocurre en $(4, 2)$ y $(2, 0)$ como se muestra en la siguiente figura.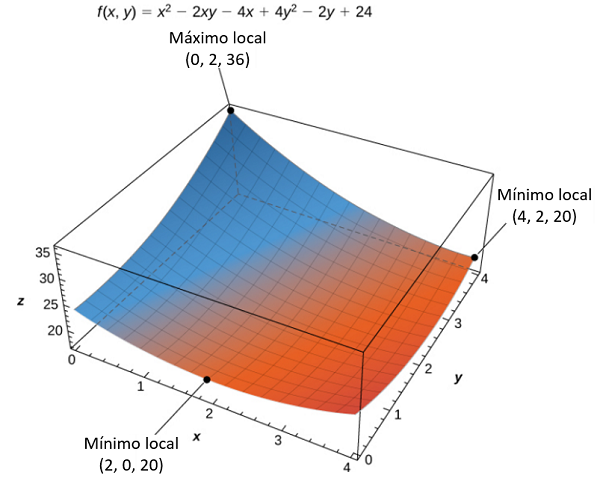

Figura 4.53. La función $f (x, y)$ tiene dos mínimos globales y un máximo global sobre su dominio.
Usando la estrategia de resolución de problemas, el paso 1 implica encontrar los puntos críticos de $g$ en su dominio. Por lo tanto, primero calculamos $g_x (x, y)$ y $g_y (x, y)$, luego los igualamos a cero:
$$g_x(x, y) = 2x + 4$$ $$g_y(x, y) = 2y − 6$$ Al igualarlos en cero, se obtiene el sistema de ecuaciones.
$$\begin{aligned} 2x + 4 &= 0\\ 2y − 6 &= 0. \end{aligned}$$ La solución a este sistema es $x = −2$ e $y = 3$. Por lo tanto, $(−2, 3)$ es un punto crítico de $g$. Calculando $g (−2, 3)$, obtenemos
$$g(−2, 3) = (−2)^2 + 3^2 + 4(−2) − 6(3) = 4 + 9 − 8 − 18 = −13.$$ El siguiente paso consiste en encontrar los extremos de $g$ en el límite de su dominio. El límite de su dominio consiste en un círculo de radio $4$ centrado en el origen como se muestra en el siguiente gráfico.

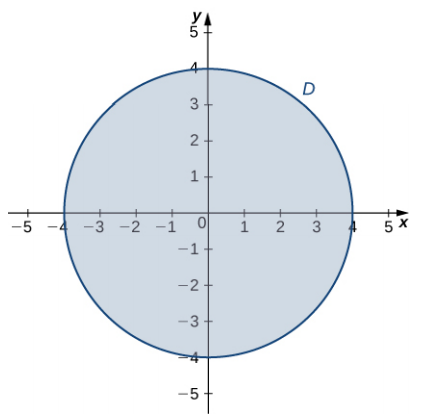
Figura 4.54. Gráfica del dominio de la función $g(x, y) = x^2 + y^2 + 4x − 6y$

El límite del dominio de $g$ puede parametrizarse utilizando las funciones $x (t) = 4 cos t, y (t) = 4 sen t$ para $0 \le t \le 2\pi$. Definamos $h (t) = g \big(x (t), (t)\big)$:
$$\begin{aligned} ht &= g \big(x (t), (t)\big)\\ &= (4 cos t)^2 + (4 sen t)^2 + 4(4 cos t) − 6(4 sen t)\\ &= 16cos^2t + 16sen^2t + 16 cos t − 24 sen t\\ &= 16 + 16 cos t − 24 sen t \end{aligned}$$ El establecer $h^{\prime}(t) = 0$ conduce a
$$\begin{aligned} −16 sen t − 24 cos t &= 0\\ \frac{-16sen t}{-16 cos t} &= \frac{24cos t}{-16 cos t}\\ tan\text{ } t &= -\frac32 \end{aligned}$$ Esta ecuación tiene dos soluciones en el intervalo $0 \le t \le 2\pi$. Uno es $t = \pi - arctan \big(\frac32\big)$ y el otro es $t = 2\pi - arctan \big(\frac32\big)$. Para el primer ángulo,
$$\begin{aligned} sen t &= sen\bigg(\pi - arctan\bigg(\frac32\bigg)\bigg) = sen\bigg(arctan\bigg(\frac32\bigg)\bigg) = \frac{3\sqrt{3}}{13}\\ cos t &= cos\bigg(\pi - arctan\bigg(\frac32\bigg)\bigg) = -cos\bigg(arctan\bigg(\frac32\bigg)\bigg) = -\frac{2\sqrt{3}}{13} \end{aligned}$$ Por lo tanto, $x(t) = 4 cos t = -\frac{8\sqrt{3}}{13}$ y $y(t) = 4 sen t = \frac{12\sqrt{3}}{13}$; es decir, $\big(-\frac{8\sqrt{3}}{13}, \frac{12\sqrt{3}}{13}\big)$ es un punto crítico en el límite, y
$$\begin{aligned} g\bigg(-\frac{8\sqrt{3}}{13}, \frac{12\sqrt{3}}{13}\bigg) &= \bigg(-\frac{8\sqrt{3}}{13}\bigg)^2 + \bigg(\frac{12\sqrt{3}}{13}\bigg)^2 +4\bigg(-\frac{8\sqrt{3}}{13}\bigg) - 6\bigg(\frac{12\sqrt{3}}{13}\bigg)\\ &= \frac{144}{13} + \frac{64}{13} - \frac{32\sqrt{13}}{13} - \frac{72\sqrt{13}}{13}\\ &= \frac{208 - 104\sqrt{13}}{13} \approx -12.844 \end{aligned}$$ Para el segundo ángulo,
$$\begin{aligned} sen t &= sen\bigg(2\pi - arctan\bigg(\frac32\bigg)\bigg) = -sen\bigg(arctan\bigg(\frac32\bigg)\bigg) = -\frac{3\sqrt{3}}{13}\\ cos t &= cos\bigg(2\pi - arctan\bigg(\frac32\bigg)\bigg) = cos\bigg(arctan\bigg(\frac32\bigg)\bigg) = \frac{2\sqrt{3}}{13} \end{aligned}$$ Por lo tanto, $x(t) = 4 cos t = \frac{8\sqrt{3}}{13}$ y $y(t) = 4 sen t = -\frac{12\sqrt{3}}{13}$; es decir, $\big(\frac{8\sqrt{3}}{13}, -\frac{12\sqrt{3}}{13}\big)$ es un punto crítico en el límite, y
$$\begin{aligned} g\bigg(\frac{8\sqrt{3}}{13}, -\frac{12\sqrt{3}}{13}\bigg) &= \bigg(\frac{8\sqrt{3}}{13}\bigg)^2 + \bigg(-\frac{12\sqrt{3}}{13}\bigg)^2 +4\bigg(\frac{8\sqrt{3}}{13}\bigg) - 6\bigg(-\frac{12\sqrt{3}}{13}\bigg)\\ &= \frac{144}{13} + \frac{64}{13} + \frac{32\sqrt{13}}{13} + \frac{72\sqrt{13}}{13}\\ &= \frac{208 + 104\sqrt{13}}{13} \approx 44.844 \end{aligned}$$ El mínimo absoluto de $g$ es $−13$, que se alcanza en el punto $(−2, 3)$, que es un punto interior de $D$. El máximo absoluto de $g$ es aproximadamente igual a 44.844, que se alcanza en el punto límite $\big(\frac{8\sqrt{3}}{13}, -\frac{12\sqrt{3}}{13}\big)$. Estos son los extremos absolutos de g en D como se muestra en la siguiente figura.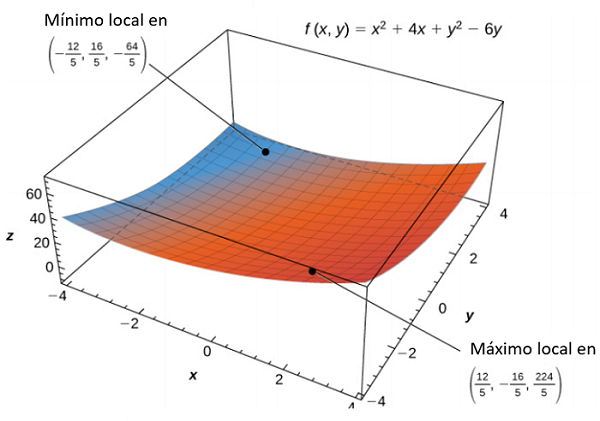

Figura 4.55. La función $f (x, y)$ tiene un mínimo local y un máximo local.