Solución

1. El paso 1 de la estrategia de resolución de problemas consiste en encontrar los puntos críticos de $f$. Para hacer esto, primero calculamos $f_x (x, y)$ y $f_y (x, y)$, luego establecemos que cada uno de ellos sea igual a cero:
   $$f_x(x, y) = 8x + 8$$ $$f_y(x, y) = 18y − 36$$ Al igualarlos a cero, se obtiene el sistema de ecuaciones:
   $$\begin{aligned} 8x + 8 &= 0\\ 18y − 36 &= 0 \end{aligned}$$ La solución a este sistema es $x = −1$ e $y = 2$. Por lo tanto $(−1, 2)$ es un punto crítico de $f$. El paso 2 de la estrategia de resolución de problemas implica calcular $D$. Para hacer esto, primero calculamos las segundas derivadas parciales de $f$:
   $$\begin{aligned} f_{xx} (x, y) &= 8\\ f_{xy} (x, y) &= 0\\ f_{yy} (x, y) &= 18 \end{aligned}$$ Por lo tanto, $D = f_{xx} (−1, 2) f_{yy} (−1, 2) - \big(f_{xy} (−1, 2)\big) 2 = (8) (18) - (0)^2 = 144$.
   El paso 3 establece verificar el teorema de Fermat para las funciones de dos variables. Como $D\gt 0$ y $f_{xx} (−1, 2)\gt 0$, esto corresponde al caso 1. Por lo tanto, $f$ tiene un mínimo local en $(−1, 2)$ como se muestra en la siguiente figura.
   

   

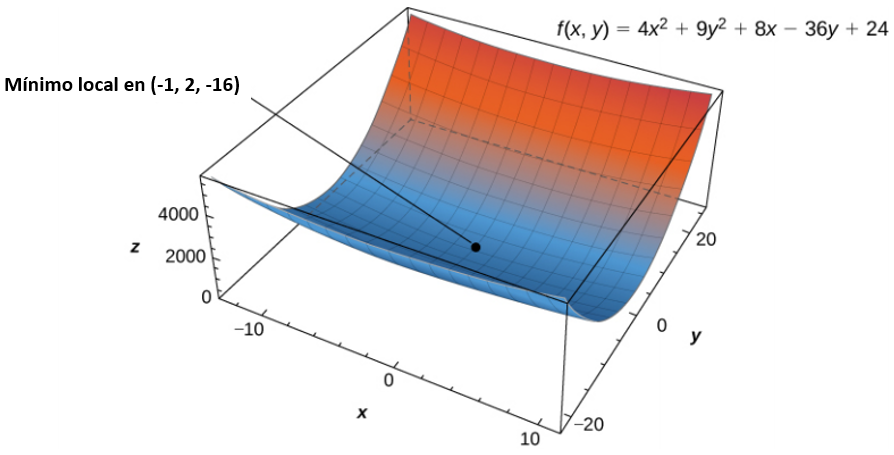
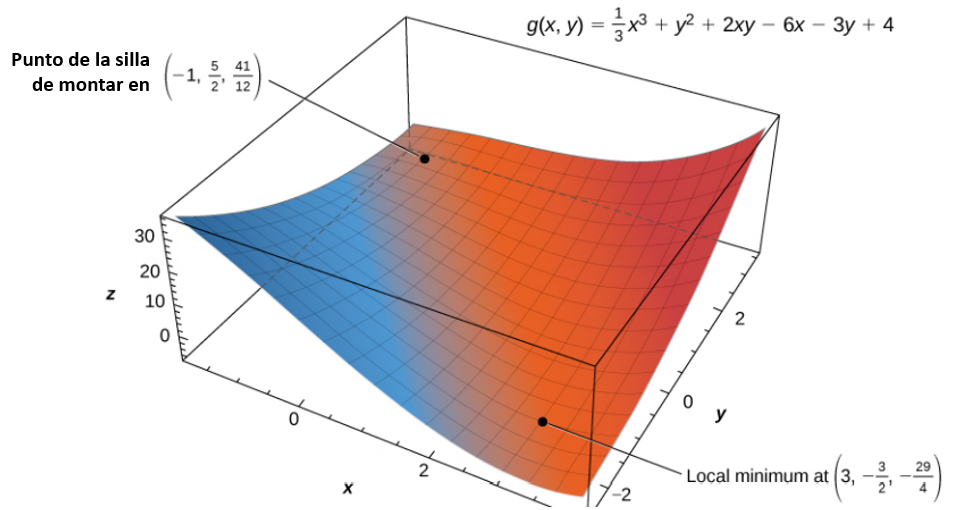
   Figura 4.50. La función $f (x, y)$ tiene un mínimo local en $(−1, 2, −16)$.

2. Para el paso 1, primero calculamos $g_x (x, y)$ y $g_y(x, y)$, luego igualamos cada uno de ellos a cero:
   $$g_x(x, y) = x^2 + 2y − 6$$ $$g_y(x, y) = 2y + 2x − 3$$ Al igualarlas a cero, se obtiene el siguiente sistema de ecuaciones:
   $$\begin{aligned} x^2 + 2y − 6 &= 0\\ 2y + 2x − 3 &= 0 \end{aligned}$$ Para resolver este sistema, primero resolvemos la segunda ecuación para $y$. Esto da $y = \frac{3 - 2x}{2}$. Sustituyendo en la primera ecuación obtenemos
   $$\begin{aligned} x^2 + 3 − 2x − 6 &= 0\\ x^2 − 2x − 3 &= 0\\ (x − 3)(x + 1) &= 0 \end{aligned}$$ Por lo tanto, $x = −1$ o $x = 3$. Al sustituir estos valores en la ecuación $y = \frac{3 - 2x}{2}$ se obtienen los puntos críticos $\big(−1, \frac52\big)$ y $\big(3, −\frac32\big)$.
   El paso 2 implica calcular las segundas derivadas parciales de $g$:
   $$\begin{aligned} g_{xx} (x, y) &= 2x\\ g_{xy} (x, y) &= 2\\ g_{yy} (x, y) &= 2 \end{aligned}$$ Luego, encontramos una fórmula general para D:
   $$\begin{aligned} D &= g_{xx} (x_0, y_0)g_{yy} (x_0, y_0) − \big(g_{xy} (x_0, y_0)\big)^2\\ &= \big(2x_0\big)(2) − 2^2\\ &= 4x_0 − 4 \end{aligned}$$ A continuación, sustituimos cada punto crítico en esta fórmula:
   $$\begin{aligned} D\bigg(−1, \frac52\bigg) &= 2(−1)(2) − (2)^2 = −4 − 4 = −8\\ D\bigg(3, -\frac32\bigg) &= 2(3)(2) − (2)^2 = 12 − 4 = 8 \end{aligned}$$ En el paso 3, observamos que, aplicando el teorema de Fermat para funciones de dos variables al punto $\bigg(−1, \frac52\bigg)$ conduce al caso 3, lo que significa que $\bigg(−1, \frac52\bigg)$ es un punto de la silla de montar. Aplicar el teorema al punto $\bigg(3, -\frac32\bigg)$ conduce al caso 1, lo que significa que $\bigg(3, -\frac32\bigg)$ corresponde a un mínimo local como se muestra en la siguiente figura.
   

   

   Figura 4.51. La función $g (x, y)$ tiene un mínimo local y un punto de la silla.