Primero, debemos calcular $\nabla f (x, y)$:
$$f_x(x, y) = 4x − 3y + 2 \text{ y } f_y = −3x + 16y − 4 \text{ entonces } \nabla f(x, y) = (4x − 3y + 2)\bold{i} + (−3x + 16y − 4)\bold{j}$$A continuación, evaluamos $\nabla f (x, y)$ en $(−2, 1)$:
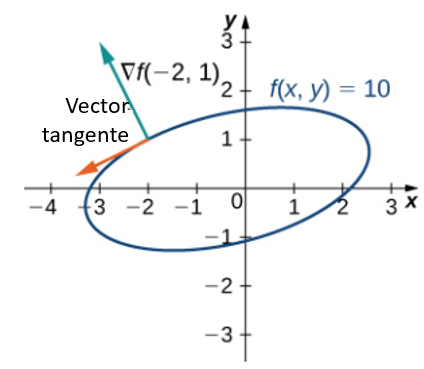
$$\nabla f(−2, 1) = \big(4(−2) − 3(1) + 2\big)\bold{i} + \big(−3(−2) + 16(1) − 4\big)\bold{j} = −9\bold{i} + 18\bold{j}$$Este vector es ortogonal a la curva en el punto $(−2, 1)$. Podemos obtener un vector tangente invirtiendo los componentes y multiplicando cualquiera de ellos por $−1$. Así, por ejemplo, $−18\bold{i} - 9\bold{j}$ es un vector tangente (ver el siguiente gráfico).

Figura 4.45. Vectores tangentes y normales a $2x^2 - 3xy + 8y^2 + 2x - 4y + 4 = 18$ en el punto $(−2, 1)$.