Solución

1. Primero, calculamos $f_x (x, y)$ y $f_y (x, y)$:
   $$\begin{aligned} f_x(x, y) &= \frac12 (−18x + 36)\big(4y^2 − 9x^2 + 24y + 36x + 36\big)^{-1/2}\\ &= \frac{-9x+18}{\sqrt{4y^2 − 9x^2 + 24y + 36x + 36}} \end{aligned}$$ $$\begin{aligned} f_y(x, y) &= \frac12 (8y + 24)\big(4y^2 − 9x^2 + 24y + 36x + 36\big)^{-1/2}\\ &= \frac{4y+12}{\sqrt{4y^2 − 9x^2 + 24y + 36x + 36}} \end{aligned}$$ A continuación, igualamos cada una de estas expresiones a cero: $$\frac{-9x+18}{\sqrt{4y^2 − 9x^2 + 24y + 36x + 36}} = 0$$ $$\frac{4y+12}{\sqrt{4y^2 − 9x^2 + 24y + 36x + 36}} = 0$$ Luego, multiplicamos cada ecuación por su común denominador: $$-9x+18=0$$ $$4y+12=0$$ Por lo tanto, $x = 2$ e $y = −3$, entonces $(2, −3)$ es un punto crítico de $f$.
   
   También debemos verificar la posibilidad de que el denominador de cada derivada parcial sea igual a cero, lo que hace que la derivada parcial no exista. Como el denominador es el mismo en cada derivada parcial, solo necesitamos hacer esto una vez:
   $$4y^2 − 9x^2 + 24y + 36x + 36 = 0$$ Esta ecuación representa una hipérbola. También debemos notar que el dominio de $f$ consiste en puntos que satisfacen la desigualdad $$4y^2 − 9x^2 + 24y + 36x + 36 \ge 0$$ Por lo tanto, cualquier punto de la hipérbola no solo es un punto crítico, sino que también se encuentra en el límite del dominio. Para poner la hipérbola en forma estándar, utilizamos el método de completar el cuadrado: $$\begin{aligned} 4y^2 − 9x^2 + 24y + 36x + 36 &= 0\\ 4y^2 − 9x^2 + 24y + 36x &= -36\\ 4y^2 + 24y − 9x^2 + 36x &= -36\\ 4\big(y^2 + 6y\big) − 9\big(x^2 − 4x\big) &= −36\\ 4(y^2 + 6y + 9) − 9(x^2 − 4x + 4) &= −36 + 36 − 36\\ 4(y+3)^2-9(x-2)^2 &= -36 \end{aligned}$$ Dividiendo ambos miembros por −36 obtenemos la ecuación en forma estándar:
   $$\begin{aligned} \frac{4(y+3)^2}{-36} - \frac{9(x-2)^2}{-36} &= 1\\ \frac{(x-2)^2}{4} - \frac{(y+3)^2}{9} &= 1 \end{aligned}$$ Observa que el punto $(2, −3)$ es el centro de la hipérbola.



2. Primero, calculamos $g_x(x, y)$ y $g_y(x, y)$:
   $$g_x(x, y) = 2x+2y+4$$ $$g_y(x, y = 2x-8y-6$$ A continuación, igualamos cada una de estas expresiones a cero, lo que da un sistema de ecuaciones en $x$ e $y$:
   $$2x+2y+4=0$$ $$2x-8y-6=0$$ Restando la segunda ecuación de la primera da $10y + 10 = 0$, entonces $y = −1$. Sustituyendo esto en la primera ecuación se obtiene $2x + 2 (−1) + 4 = 0$, entonces $x = −1$. Por lo tanto $(−1, −1)$ es un punto crítico de g (Figura 4.46). No hay puntos en $\Reals^2$ que hacen que no exista ninguna derivada parcial
   

   

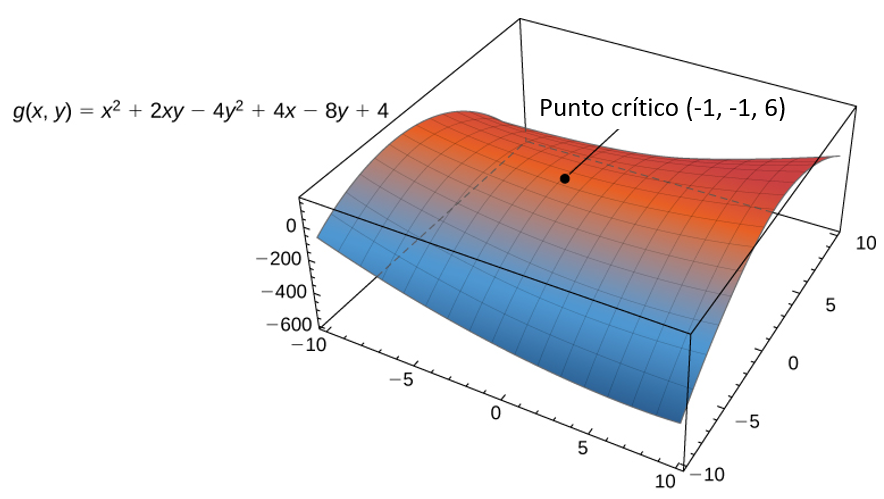
   Figura 4.46. La función $g (x, y)$ tiene un punto crítico en $(−1, −1, 6)$.