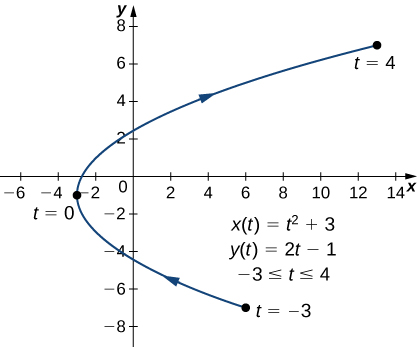
Apartado a
Para aplicar la ecuación, primero calcula $x'(t)$ e $y'(t)$:
$$x'(t) = 2t, \;\;\;\;y'(t) = 2$$ $${{dy} \over {dx}} = {{dy/dt} \over {dx/dt}} = {{y'\left( t \right)} \over {x'\left( t \right)}}{\rm{ }} \Rightarrow {{dy} \over {dx}} = {2 \over {2t}} \Rightarrow {{dy} \over {dx}} = {1 \over t}$$
Figura. Gráfico de la curva descrita por ecuaciones paramétricas en la parte a.
Apartado b
Para aplicar la ecuación, primero calcula $x'(t)$ e $y'(t)$:
$$x'(t) = 2 \;\;\;\;y'\left( t \right) = 3{t^2} - 3$$
Luego sustituye en la ecuación:
$$\frac{{dy}}{{dx}} = \frac{{dy/dt}}{{dx/dt}} = \frac{{y'\left( t \right)}}{{x'\left( t \right)}}{\text{ }} \Rightarrow \frac{{dy}}{{dx}} = \frac{{3{t^2} - 3}}{2}$$Esta derivada es cero cuando $t = ± 1$.
Cuando $t = −1$ tenemos $$x(−1) = 2\cdot(−1) + 1 = −1 $$ $$y\left( { - 1} \right) = {\left( { - 1} \right)^3} - 3 \cdot \left( { - 1} \right) + 4 = - 1 + 3 + 4 = 6$$,
que corresponde al punto $(−1, 6)$ en la gráfica.
Cuando $t = 1$ tenemos
$$x( 1) = 2 \cdot 1 + 1 = 3$$ $$y\left( 1 \right) = {1^3} - 3 \cdot 1 + 4 = 1 - 3 + 4 = 2$$que corresponde al punto $(3, 2)$ en la gráfica. El punto $(3, 2)$ es un mínimo relativo y el punto $(−1, 6)$ es un máximo relativo, como se ve en el siguiente gráfico.
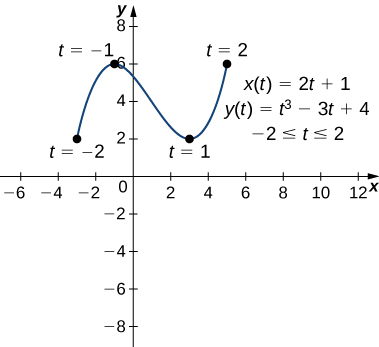
Figura. Gráfico de la curva descrita por ecuaciones paramétricas en la parte b.
Apartado c
Para aplicar la ecuación, primero calcula $x'(t)$ e $y'(t)$:
$$x'(t) = - 5sent \;\;\;\;y'(t) = 5cost$$
Luego sustituye en la ecuación:
$$\frac{{dy}}{{dx}} = \frac{{dy/dt}}{{dx/dt}} = \frac{{y'\left( t \right)}}{{x'\left( t \right)}}{\text{ }} \Rightarrow \frac{{dy}}{{dx}} = \frac{{5\cos t}}{{ - 5sent}} = - \cot \,t$$Esta derivada es cero cuando $cost = 0$ y no está definida cuando $sent = 0$. Esto da $t = 0$, $\pi/2$, $\pi$, $3\pi/2$ y $2\pi$ como puntos críticos para $t$. Sustituyendo cada uno de ellos en $x(t)$ e $y(t)$, obtenemos
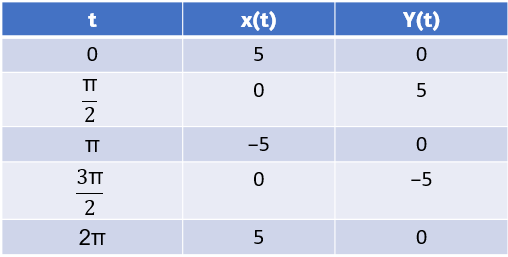
Estos puntos corresponden a los lados, arriba y abajo del círculo que se representa mediante las ecuaciones paramétricas (ver la siguiente figura). En los bordes izquierdo y derecho del círculo, la derivada no está definida, y en la parte superior e inferior, la derivada es igual a cero.
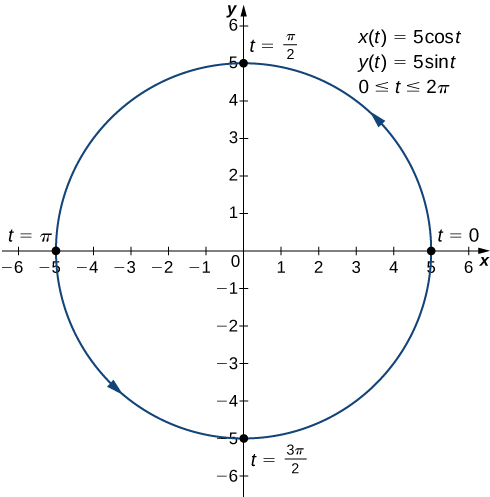
Figura. Gráfico de la curva descrita por ecuaciones paramétricas en la parte c.