Apartado a
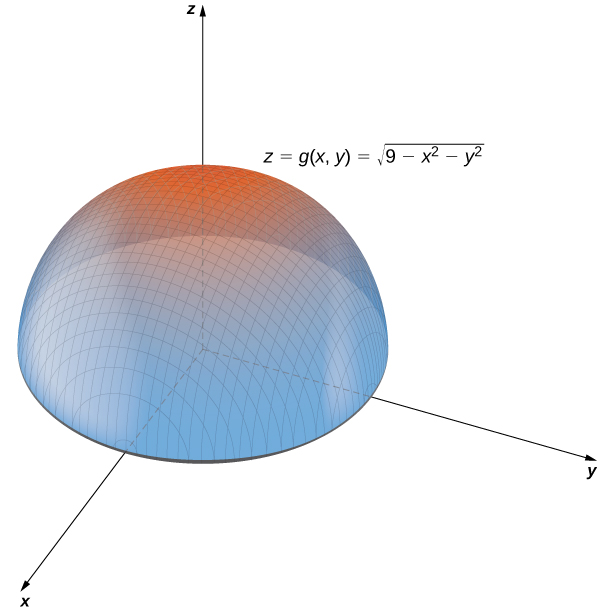
En el ejercicio anterior, determinamos que el dominio de $g (x, y) = \sqrt{9 − x^2 − y^2 }$ es $\{(x, y) \isin \Reals^2|x^2 + y^2\le 9\}$ y el rango es $\{z \isin \Reals^2|0\le z\le 3\}$.
Cuando $x^2 + y^2 = 9$ tenemos $g (x, y) = 0$. Por lo tanto, cualquier punto del círculo de radio $3$ centrado en el origen en el plano $xy$ se asigna a $z = 0$ en $\Reals^3$.
Si $x^2 + y^2 = 8$, entonces $g (x, y) = 1$, entonces cualquier punto en el círculo de radio $2\sqrt{2}$ centrado en el origen en el plano $xy$, se asigna a $z = 1$ en $\Reals^3$.
A medida que $x^2 + y^2$ se acerca a cero, el valor de $z$ se aproxima a $3$. Cuando $x^2 + y^2 = 0$, entonces $g (x, y) = 3$. Este es el origen en el plano $xy$. Si $x^2 + y^2$ es igual a cualquier otro valor entre $0$ y $9$, entonces $g (x, y)$ es igual a alguna otra constante entre $0$ y $3$. La superficie descrita por esta función es una semiesfera centrada en el origen con radio $3$ como se muestra en el siguiente gráfico.

Figura 4.4 Gráfico del hemisferio representado por la función dada de dos variables.
Apartado b
Esta función también contiene la expresión $x^2 + y^2$. Al cortar esta superficie por varios planos paralelos a $xy$, $z=k$, obtenemos círculos de radio creciente a medida que $k$ aumenta. El valor mínimo de $f (x, y) = x^2 + y^2$ es cero (alcanzado cuando $x = y = 0$).
Cuando $x = 0$, la función se convierte en $z = y^2$. Cuando $y = 0$, entonces la función se convierte en $z = x^2$. Estas son secciones transversales del gráfico y son parábolas. Recuerda de la introducción a los vectores en el espacio que el nombre de la gráfica de $f (x, y) = x^2 + y^2$ es un paraboloide. El gráfico de $f$ aparece en el siguiente gráfico.
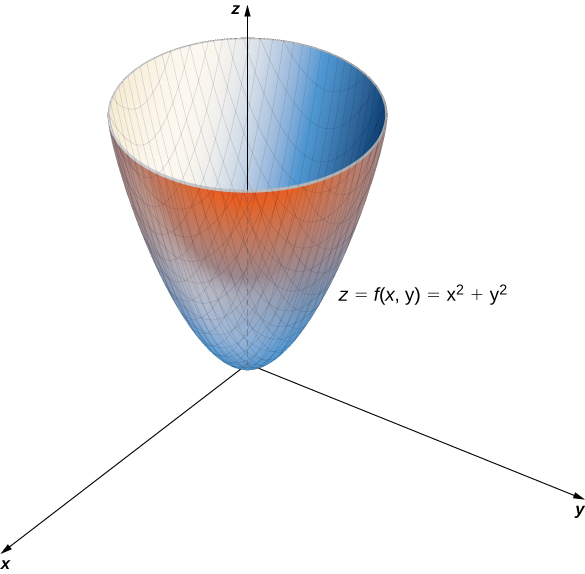
Figura 4.5 Un paraboloide es el gráfico de la función dada de dos variables.