Ejemplo 1

$$r_1:\left(x,y,z\right)=\left(1,1,1\right)+t\left(0,1,2\right)$$

$r_2:$Recta que pasa por$A\left(0,1,-1\right)yB\left(1,2,z_0\right)$

Hallar $z_0$ para que las rectas sean concurrentes y encontrar el plano que las contiene.

Resolución

Construyamos una ecuación vectorial de la recta $r_2$:

Escribimos las ecuaciones paramétricas de cada recta:

$$r_1:\{\begin{array}{c}x=1\\ y=1+t\\ z=1+2t\end{array},r_2:\{\begin{array}{c}x=\lambda \\ y=1+\lambda \\ z=-1+\left(1+z_0\right)\lambda \end{array}$$

Igualamos:

$$\{\begin{array}{c}1=\lambda \\ 1+t=1+\lambda \\ 1+2t=-1+\lambda \left(z_0+1\right)\end{array}$$

De las dos primeras ecuaciones, se obtiene $t=\lambda =1$

Reemplazamos en la tercera ecuación y despejamos $z_0$:

$$3=-1+z_0+1\Rightarrow z_0=3$$

Para $z_0=3$ las rectas se cortan.

¿Cuál es el punto de intersección? Reemplazamos por $t=1$ en la ecuación de la primera recta:

$$r_1\cap r_2=\left\{\left(1,2,3\right)\right\}$$

Para obtener la ecuación del plano que contiene a las rectas, buscamos el vector normal:

$$\overrightarrow{n}=\overrightarrow{v_1}\times \overrightarrow{v_2}=\left|\begin{array}{ccc}i& j& k\\ 0& 1& 2\\ 1& 1& 4\end{array}\right|=\left(2,2,-1\right)$$

$$\pi :2x+2y-z+d=0$$

Para averiguar $d$ reemplazamos un punto que pertenezca al plano. Puede ser cualquier punto de las rectas, por ejemplo $\left(1,1,1\right)$:

$$2.1+2.1-1.1+d=0\Rightarrow d=-3$$

$$\pi :2x+2y-z-3=0$$

Ejemplo 2

$$r_1:\left(x,y,z\right)=\left(1,2,3\right)+\lambda \left(-1,1,4\right)$$

$$r_2:\left(x,y,z\right)=\left(1,0,0\right)+t\left(3,-3,-12\right)$$

Claramente son paralelas pues sus vectores directores son paralelos:

$\left(3,-3,-12\right)=-3.\left(-1,1,4\right)$.

El lector puede comprobar que $\left(-1,1,4\right)\times \left(3,-3,-12\right)=\overrightarrow{0}$ , entonces el vector normal del plano no puede hallarse con este producto vectorial.

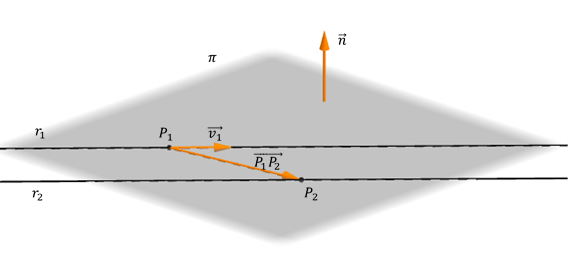
Para hallar el vector normal, consideramos uno de los vectores directores y un vector $\overrightarrow{P_1{P}_2}$ determinado por un punto de cada recta, como muestra la figura:

El producto vectorial de ambos da un vector normal al plano:

$$\overrightarrow{n}=\overrightarrow{v}\times \overrightarrow{P_1{P}_2}$$

Para completar la ecuación del plano, consideramos un punto de cualquiera de las rectas. Así obtenemos la ecuación del plano que contiene a las rectas dadas:

$$\pi :5x-3y+2z-5=0$$

Ejemplo 3

Hallar, si es posible, el plano que contiene a las rectas:

$$r_1:\left(x,y,z\right)=\lambda \left(1,0,0\right)$$

$$r_2:\left(x,y,z\right)=\left(0,1,0\right)+t\left(0,0,1\right)$$

Dejamos a cargo del lector la verificación de que son alabeadas. Busquemos un vector perpendicular a ambas rectas:

$$\overrightarrow{n}=\left(1,0,0\right)\times \left(0,0,1\right)=\left(0,-1,0\right)$$

Considerando el punto $\left(0,0,0\right)$ perteneciente a $r_1$, obtenemos el siguiente plano:

$$\pi :y=0$$

Sin embargo, este plano no contiene a $r_2$, pues el punto $\left(0,1,0\right)$ no verifica la ecuación de $\pi$.

Sugerimos al lector hacer una gráfico de las rectas y el plano obtenido, para visualizar la situación.

No es posible hallar un plano que contenga a dos rectas alabeadas. Las rectas alabeadas no son coplanares.