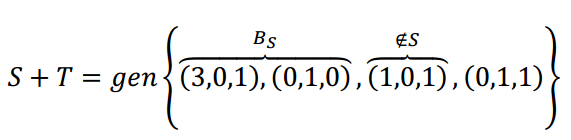
Dados los siguientes subespacios de \(V = {\mathbb{R}^3}\):
\[S = \left\{ {\left( {x,y,z} \right)|\;x - 3z = 0} \right\}\]
\[T = \left\{ {\left( {x,y,z} \right)|\;x \; + \; y \;-\; z = 0} \right\}\]
Nos interesa hallar \(S + T\).
Busquemos una base de \(S\). Para eso en la ecuación despejamos una variable:
\[x = 3z\]
Ahora armamos un vector genérico:
\[\left( {x,y,z} \right) = \left( {3z,y,z} \right) = z\left( {3,0,1} \right) + y\left( {0,1,0} \right)\]
\[{B_S} = \left\{ {\left( {3,0,1} \right),\left( {0,1,0} \right)} \right\}\]
Busquemos una base de \(T\). Para esto en la ecuación despejamos una variable:
\[z = x + y\]
Ahora armamos un vector genérico:
\[\left( {x,y,z} \right) = \left( {x,y,x + y} \right) = x\left( {1,0,1} \right) + y\left( {0,1,1} \right)\]
Entonces
\[{B_T} = \left\{ {\left( {1,0,1} \right),\left( {0,1,1} \right)} \right\}\]
\[S + T = gen\left\{ {\left( {3,0,1} \right),\left( {0,1,0} \right),\left( {1,0,1} \right),\left( {0,1,1} \right)} \right\}\]
Sabemos que todo conjunto de más de 3 vectores en \({\mathbb{R}^3}\) es linealmente dependiente, ya que la dimensión de \({\mathbb{R}^3}\) es 3. ¿Cómo podemos extraer una base de la suma?
Podríamos armar una matriz con estos 4 vectores y llevarla a la forma escalonada. O si no, como el espacio es \({\mathbb{R}^3}\) podemos pensar geométricamente:
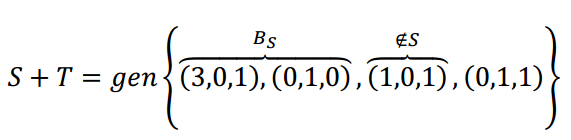
Por lo tanto: \(B = \left\{ {\left( {3,0,1} \right),\left( {0,1,0} \right),\left( {1,0,1} \right)} \right\}\) es base de \(S + T\) y es base de \(\mathbb{R}^3\).
En este caso, como \(S + T\;\) es un subespacio de \({R^3}\) de dimensión 3, podemos afirmar que:
\[S + T = {\mathbb{R}^3}\]
Generalizando:
\(S\) subespacio de \(V\) y \(\dim \left( S \right) = \dim \left( V \right) \Rightarrow S = V\)
Dados los siguientes subespacios de \(V = {\mathbb{R}^4}\):
\[{S_1} = \left\{ {x \in {\mathbb{R}^4}|\;{x_1} + {x_2} = {x_2} + {x_4} = 0} \right\}\]
\[{S_2} = \left\{ {x \in {\mathbb{R}^4}|\;{x_1} – {x_4} = {x_3} + {x_4} = 0} \right\}\]
Hallar base y dimensión de \({S_1} + {S_2}\;\).
\[\left( {{x_1},{x_2},{x_3},{x_4}} \right) = \left( { – {x_2},{x_2},{x_3}, – {x_2}} \right) = {x_2}\left( { – 1,1,0, – 1} \right) + {x_3}\left( {0,0,1,0} \right)\]
\[{B_{{S_1}}} = \left\{ {\left( {1, – 1,0,1} \right),\left( {0,0,1,0} \right)} \right\}\]
\[\left( {{x_1},{x_2},{x_3},{x_4}} \right) = \left( {{x_4},{x_2}, – {x_4},{x_4}} \right) = {x_4}\left( {1,0, – 1,1} \right) + {x_2}\left( {0,1,0,0} \right)\]
\[{B_{{S_2}}} = \left\{ {\left( {1,0, – 1,1} \right),\left( {0,1,0,0} \right)} \right\}\]
\[{S_1} + {S_2} = gen\left\{ {\left( {1, – 1,0,1} \right),\left( {0,0,1,0} \right),\left( {1,0, – 1,1} \right),\left( {0,1,0,0} \right)} \right\}\]
Cómo hemos visto, un método para analizar si son LI o LD, consiste en armar una matriz con los vectores como filas y llevarla a su forma escalonada. Por conveniencia colocaremos los vectores en el siguiente orden:
\(\left( {\begin{array}{*{20}{c}}1&{ – 1}&0&1\\1&0&{ – 1}&1\\0&1&0&0\\0&0&1&0\end{array}} \right)\)
\(\mathop \to \limits_{{F_2} \;\; \to \; {F_2} \; - \; {F_1}} \; \left( {\begin{array}{*{20}{c}}1&{ – 1}&0&1\\0&1&{ – 1}&0\\0&1&0&0\\0&0&1&0\end{array}} \right)\)
\(\mathop \to \limits_{{F_3} \;\; \to \; {F_3} \; – \; {F_2}} \; \left( {\begin{array}{*{20}{c}}1&{ – 1}&0&1\\0&1&{ – 1}&0\\0&0&1&0\\0&0&1&0\end{array}} \right)\)
\(\mathop \to \limits_{{F_4} \;\; \to \; {F_4} \; – \; {F_3}} \; \left( {\begin{array}{*{20}{c}}1&{ -1}&0&1\\0&1&{ – 1}&0\\0&0&1&0\\0&0&0&0\end{array}} \right)\)
La matriz escalonada tiene 3 filas LI (su rango es 3), entonces podemos afirmar que la dimensión de \(S + T\) es 3.
Como se anuló la última fila, el vector \(\left( {0,0,1,0} \right)\) es combinación lineal de los otros tres, por lo tanto una base de \(S + T\) es: \({B_{S + T}} = \left\{ {\left( {1, -1,0,1} \right),\left( {0,1,0,0} \right),\left( {1,0, - 1,1} \right)} \right\}\).
Recordemos que las filas de la matriz escalonada componen otra base de la suma:
\[B\;'{_{S + T}} = \left\{ {\left( {1, -1,0,1} \right),\left( {0,1, -1,0} \right),\left( {0,0,1,0} \right)} \right\}\]