solución1

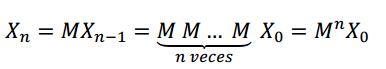
Según los datos, finalizado el 1º semestre la fracción de la clientela que tiene A puede obtenerse así:

$0, 70 a_{0} + 0, 10 b_{0} + 0, 10 c_{0} = a_{1}$

¿Qué ecuaciones permiten obtener $b_{1}$ y $c_{1}$ ?

Resulta entonces el siguiente sistema: ${\begin{matrix} 0, 70 a_{0} + 0, 10 b_{0} + 0, 10 c_{0} = a_{1} \\ 0, 15 a_{0} + 0, 85 b_{0} + 0, 10 c_{0} = b_{1} \\ 0, 15 a_{0} + 0, 05 b_{0} + 0, 80 c_{0} = c_{1} \end{matrix}$

El lector puede comprobar que este sistema puede expresarse mediante un producto de matrices como sigue:

$(\begin{matrix} 0, 70 & 0, 10 & 0, 10 \\ 0, 15 & 0, 85 & 0, 10 \\ 0, 15 & 0, 05 & 0, 80 \end{matrix}) (\begin{matrix} a_{0} \\ b_{0} \\ c_{0} \end{matrix}) = (\begin{matrix} a_{1} \\ b_{1} \\ c_{1} \end{matrix})$

O sea: $M X_{0} = X_{1} [1]$

La matriz $M \in R^{3 \times 3}$ , que caracteriza la evolución del sistema, se denomina matriz de transición.

¿Qué características presenta esta matriz de transición?

1) Todos sus elementos son números reales comprendidos entre 0 y 1.

2) La suma de los elementos de cada columna es 1.

Las matrices cuadradas que cumplen estas dos condiciones se denominan matrices estocásticas o matrices de probabilidad.

Como la matriz de transición se mantiene para el 2º período, la fracción de clientes para el tiempo $t = 2$ puede calcularse como:

$M X_{1} = X_{2} [2]$

De [1] y [2] se deduce que: $X_{2} = M^{2} X_{0}$

Si los porcentajes de cambio de clientela no cambian en los períodos siguientes, entonces $M$ no cambia cuando se pasa del estado $(n - 1$ ) al estado $n$ .

Por lo tanto:

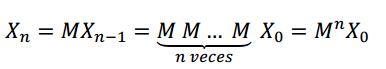
potencias de una matriz cuadrada de probabilidad

O sea, para obtener cómo se distribuyen los clientes luego de $n$ períodos, podemos proceder así:

$X_{n} = M^{n} X_{0}$

Suponiendo que inicialmente las tres empresas se reparten por partes iguales la clientela, les pedimos que calculen cómo resulta la distribución de clientes:

Al cabo de 3 años.
Al cabo de 10 años
Al cabo de 15 años

Observen luego de hacer los cálculos que en la medida en que el tiempo pasa, las cuotas de mercado de las empresas tienden a estabilizarse.

4. Responder las mismas preguntas suponiendo que inicialmente las cuotas de mercado de las empresas A, B y C son respectivamente: 0,5 , 0,35 y 0,15.

5. ¿Se produce el mismo fenómeno de estabilización en este caso?