El vector \(\left( {0,0,3} \right)\) es combinación lineal de \(\left( {0,0,1} \right)\) ya que:
\[\left( {0,0,3} \right) = 3\left( {0,0,1} \right)\]
Veamos cómo se puede pensar esto desde la perspectiva geométrica. ¿Qué vectores pueden expresarse como combinación lineal del vector \(\left( {0,0,1} \right)\)?
Todos los vectores \(\left( {0,0,k} \right)\) con \(k \in \mathbb{R}\). Es decir que todos los vectores sobre el eje \(z\), son combinación lineal de \(\left( {0,0,1} \right)\).
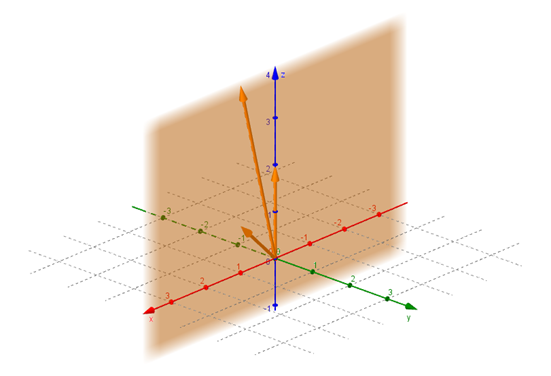
El vector \(\left( {1,0,4} \right)\) es combinación lineal de \(\left( {1,0,1} \right),\left( {0,0,2} \right)\) ya que:
\[1.\left( {1,0,1} \right) + \frac{3}{2}.\left( {0,0,2} \right) = \left( {1,0,4} \right)\]
Geométricamente el vector \(\left( {1,0,4} \right)\) es un vector coplanar con los vectores \(\left( {1,0,1} \right)\) y \(\left( {0,0,2} \right)\). Se puede ver en la siguiente gráfica que pertenecen al plano \(y = 0\):

El vector \(8x - 4{x^2}\) es combinación lineal de los vectores \(x\) y \({x^2}\) ya que:
\[8x - 4{x^2} = 8.\left( x \right) + \left( { -4} \right).{x^2}\]
¿Es el vector \(\left( {1,8} \right)\) combinación lineal de los vectores \(\left( {1,0} \right),\left( {3,3} \right)\)?
Para responder esto debemos buscar si existen escalares \(\alpha ,\beta \) tales que:
\[\left( {1,8} \right) = \alpha \left( {1,0} \right) + \beta \left( {3,3} \right)\]
\[\left\{ {\begin{array}{*{20}{c}}{1 = \alpha + 3\beta }\\{8 = 3\beta }\end{array}} \right. \Rightarrow \alpha = - 7,\;\;\;\beta = \frac{8}{3}\]
Como existen escalares que satisfacen la igualdad entonces \(\left( {1,8} \right)\) es combinación lineal de \(\left( {1,0} \right),\left( {3,3} \right)\).
¿Para qué valores de k el vector \(\left( {1,2,3} \right)\) es combinación lineal de los vectores \(\left( {1,0,0} \right),\left( {0,1,0} \right),\left( {0,2,k} \right)\)?
Para responder esto debemos buscar si existen escalares \(\alpha ,\beta ,\gamma \) tales que:
\[\left( {1,2,3} \right) = \alpha \left( {1,0,0} \right) + \beta \left( {0,1,0} \right) + \gamma \left( {0,2,k} \right)\]
\[\left\{ {\begin{array}{*{20}{c}}{\alpha = 1}\\{\beta + 2\gamma = 2}\\{\gamma k = 3}\end{array}} \right.\;\]
Si \(k = 0\) la tercera ecuación queda \(0 = 3\), y el sistema es incompatible. Si \(k \ne 0\) entonces se puede obtener \(\gamma \;{\rm{y}}\;\beta \).
Entonces para todo \(k \ne 0\) el vector \(\left( {1,2,3} \right)\) se puede expresar como combinación lineal de los vectores dados.