buscar Buscar en RED Descartes    

Sábado, 22 Octubre 2022 00:00

Como se hizo. Carga de idioma por defecto

Escrito por
Valora este artículo
(1 Voto)
Como se hizo. Carga de idioma por defecto

Por cuestiones de seguridad informática, los navegadores no permiten la lectura directa, es decir, a través de código de programación, de ficheros alojados en el equipo local del usuario.

Los juegos didácticos del Proyecto AJDA cargan el idioma de la interfaz de ficheros de texto (hay un fichero .txt para cada idioma). Cuando el juego se ejecuta desde la web de AJDA (a través de Internet) no hay problema ya que los ficheros de idioma se cargan desde el servidor web y el navegador lo permite sin problema. Sin embargo, cuando los juegos se ejecutan directamente desde el equipo local del usuario, los navegadores no permiten la carga de los ficheros de idiomas por las mencionadas cuestiones de seguridad.

Si no se carga la interfaz, el juego no puede utilizarse directamente desde el ordenador del cliente. Para solucionar este problema, los juegos se han diseñado para que el fichero de idioma por defecto (esp.txt), se cargue de forma automática al principio del juego desde la web del Proyecto ADJA, utilizando las tecnologías AJAX, tal y como comentamos a continuación.

En la cabecera de cada juego, entre las etiquetas <head> y </head>, se introduce el siguiente código javascript que comentamos a continuación:

<script>

var nombreJuego = "Nombre del fichero que contiene el juego";
var idm;

function leerIdioma(urlIDM)
{
var xmlhttp = new XMLHttpRequest();
xmlhttp.onreadystatechange = function()
     {
    if ( xmlhttp.readyState == 4 && xmlhttp.status==200 )
           {  
idm = xmlhttp.responseText;
 
      window.addEventListener("load", function(evt) 
                     {
        window.postMessage({
          type: "set",
            name: "IDMDEFECTO",
              value: idm
     }, '*');
        window.postMessage({
            type: "update"
        }, '*');
      });
        }
}
xmlhttp.open("POST", urlIDM, false);
xmlhttp.send(); 
}
var urlIDM = servidor  + rutaJuegosPrefijo + nombreJuego + rutaIdioma;
leerIdioma(urlIDM);

</script>
  • Las variables: urlIDM, servidor, rutaJuegosPrefijo, nombreJuego, rutaIdioma, sirven para indicar la ruta completa en la que se encuentra el fichero de idioma por defecto dentro de la web del Proyecto AJDA.
  • La llamada a la función leerIdioma(urlIDM) se realiza después de ser definida, por lo que se ejecuta automáticamente, pasándole como parámetro la variable que contiene la ruta del fichero de idioma que se encuentra en la web de AJDA (urlIDM).
  • La leerIdioma(urlIDM) es la que se encarga de traer los datos del fichero de idioma por defecto a través de las tecnología AJAX y su funcionamiento es el siguiente:
    • Primero se crea el objeto javascript XMLHttpRequest(), que permite traer información de una URL en segundo plano (puede traer datos de otra web).
    • Después se indica que cada vez que cambie el estado de la propiedad readyState (estado de la llamada a la información pedida) por el objeto XMLHttpRequest(), a través del evento onreadystatechange, se ejecute la siguiente función (ver siguiente punto).
    • La función en primer lugar comprueba que la respuesta es completa (xmlhttp.readyState ==4) y correcta (xmlhttp.status==200). En caso de serlo se introduce en la variable idm los datos recibidos en el objeto xmlhttp en formato texto (.responseText).
    • A continuación se desencadena un evento window.addEventListener, que pasa el valor de la variable idm a la variable IDMDEFECTO y envía el valor de IDMDEFECTO a la escena del juego que está en la misma página, en su parte <body>, a través de la instrucción  window.postMessage (que tiene el formato indicado en el código).
    • Por último se indica la forma de comunicación: método (GET/POST), dirección URL y sincronicidad (true/false, false indica que se haga de forma síncrona) (xmlhttp.open("POST", urlIDM, false)), a través de la cual se van a enviar los datos solicitados y se ordena su envío (xmlhttp.send()).
En la parte del juego, al comenzar este se ordena ejecutar automáticamente la función: FICHEROIDIOMA(), que es un algoritmo que realiza lo siguiente:
  • Introduce el valor de IDMDEFECTO en la variable cadena3b (cadena3b=IDMDEFECTO).
  • Crea la variable cadena3 que lo que hace es preparar la variable cadena3b para que pueda ser transformada en un vector (cadena3='<IDM>\n'+cadena3b+'</IDM>').
  • Convierte la variable cadena3 en el vector IDM (_StrToVector_(cadena3,'IDM')).
A partir de este momento, los valores del vector IDM (IDM[0], IDM[1], IDM[2]... ), pueden ser usados en los nombres de los controles y textos de la interfaz del juego.
Publicado en Difusión
¡Escribe el primer comentario!
Leer más ...
Jueves, 20 Octubre 2022 01:54

Comienza la III Edición del Curso para el Diseño de Objetos Interactivos con DescartesJS

Escrito por
Valora este artículo
(4 votos)
Comienza la III Edición del Curso para el Diseño de Objetos Interactivos con DescartesJS

El próximo viernes, 21 de octubre, comienza la III Edición del Curso para el Diseño de Objetos Interactivos con la Herramienta de Autor DescatesJS, que forma parte del programa de Educación Abierta de RED Descartes, con participantes de siete países de habla hispana e inglesa, con docentes y profesionales de la educación que comprenden las etapas educativas de primaria, secundaria, bachillerato y universidad, así como una amplia gama de especialidades.

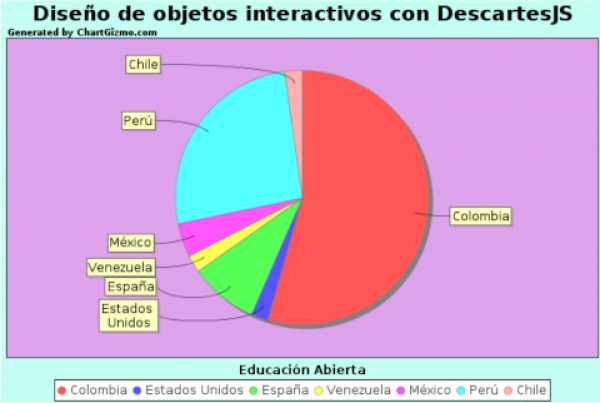
Compartimos el siguiente diagrama de sectores con el porcentaje de participación por países:

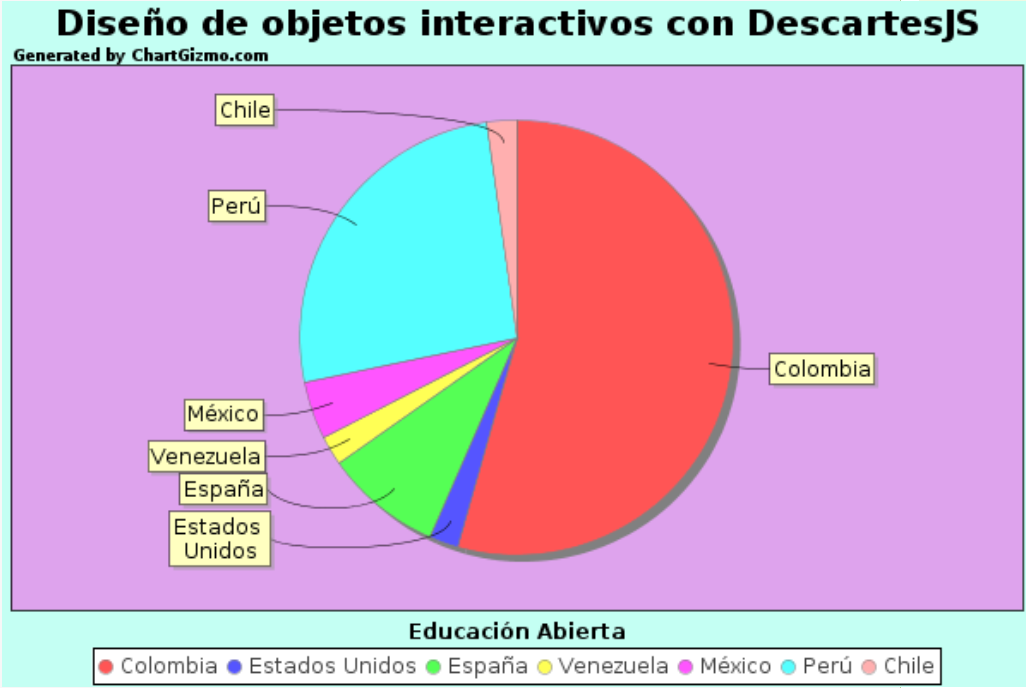
iii edicion paises

Recordamos a todos los participantes que el curso comienza el día 21 de octubre y finaliza el 3 de marzo de 2023, impartiéndose las sesiones de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al siguiente calendario previsto y contenidos a tratar: 

calendario y contenidos descartesjs

Ya hemos enviado correo personalizado a cada participante con las instrucciones correspondientes y la bienvenida al curso. No obstante si, una vez revisada la carpeta spam, no aparece el mensaje, recomendamos contactar con Educación Abierta de REDDescartes en la dirección Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo. para solventar la situación.

Quedan pocas plazas, así que aún estás a tiempo de acceder y cumplimentar el formulario de inscripción.

Os dejamos con el vídeo de presentación de esta nueva edición a cargo del Dr. D. Juan Guillermo Rivera Berrío.

Publicado en Difusión
Etiquetado como
¡Escribe el primer comentario!
Leer más ...
Martes, 11 Octubre 2022 12:24

Comienza la IV Edición del Curso para el Diseño de Libros Interactivos

Escrito por
Valora este artículo
(7 votos)
Comienza la IV Edición del Curso para el Diseño de Libros Interactivos

El próximo viernes, 14 de octubre, comienza la IV Edición del Curso para el Diseño de Libros Interactivos, que forma parte del programa de Educación Abierta de RED Descartes, con participantes de once países de habla hispana e inglesa, con docentes y profesionales de la educación que comprenden las etapas educativas de primaria, secundaria, bachillerato y universidad, así como una amplia gama de especialidades.

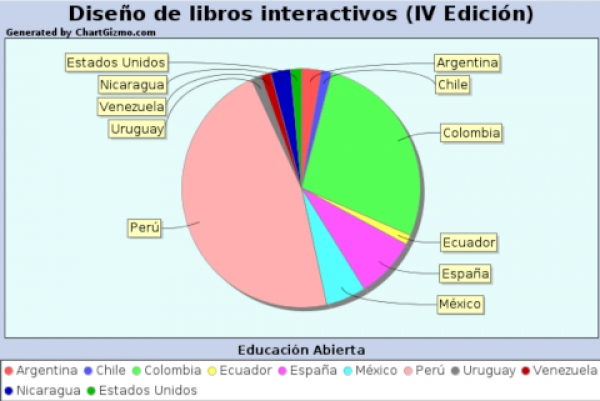
Compartimos el siguiente diagrama de sectores con el porcentaje de participación por países:

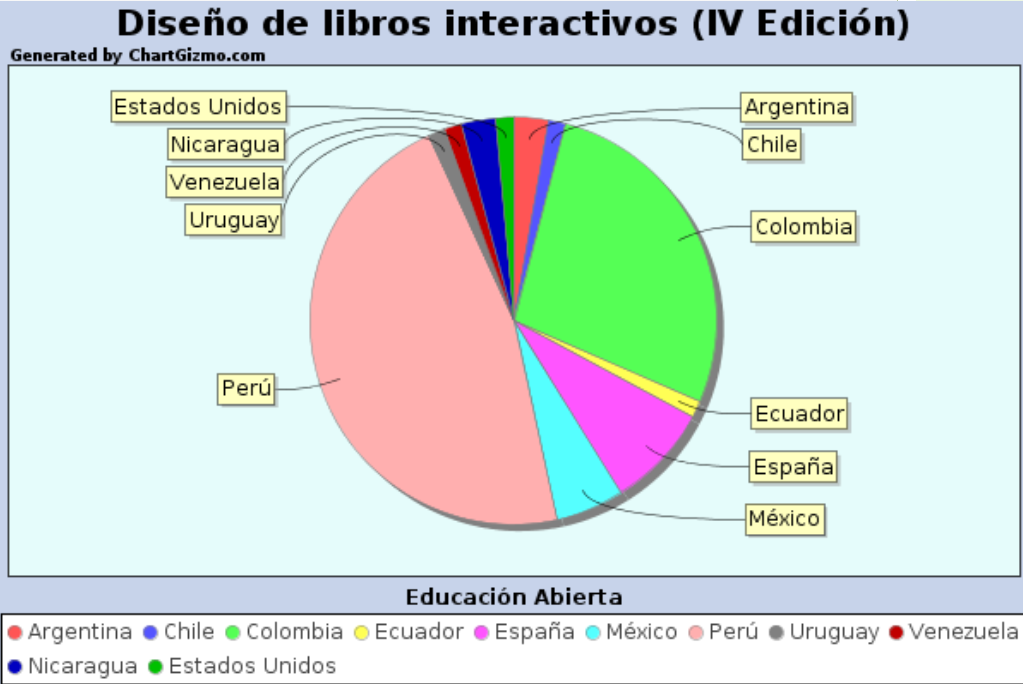
iv edicion paises

Recordamos a todos los participantes que el curso comienza el día 14 de octubre y finaliza el 17 de febrero de 2023, impartiéndose las sesiones de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al siguiente calendario previsto y contenidos a tratar:

contenidos libros 14 octubre

Ya hemos enviado correo personalizado a cada participante con las instrucciones correspondientes y la bienvenida al curso. No obstante si, una vez revisada la carpeta spam, no aparece el mensaje, recomendamos contactar con Educación Abierta de REDDescartes en la dirección Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.  para solventar la situación.

Quedan pocas plazas, así que aún estás a tiempo de acceder y cumplimentar el formulario de inscripción.

Os dejamos con el vídeo de presentación de esta nueva edición a cargo del Dr. D. Juan Guillermo Rivera Berrío.

Publicado en Difusión
Etiquetado como
¡Escribe el primer comentario!
Leer más ...
Domingo, 02 Octubre 2022 12:14

Convocatoria del curso para la edición de objetos interactivos con DescartesJS

Escrito por
Valora este artículo
(7 votos)
Convocatoria del curso para la edición de objetos interactivos con DescartesJS

El nuevo Marco de Referencia para la Competencia Digital Docente recoge, en el área 2 dedicada a contenidos digitales, entre sus elementos específicos:

  • "Utilización de herramientas de autor para la modificación, diseño y creación de contenidos educativos digitales nuevos o derivados de otros contenidos..."
  • "Aplicación de criterios de calidad de los contenidos educativos digitales para su adaptación al alumnado con el que se trabaja y a los fines perseguidos".
  • "Respeto de los derechos de autor y de las limitaciones de la propiedad intelectual aplicadas al ámbito educativo para la reutilización y la creación de contenidos..."

Pues bien, desde RED Descartes te ofrecemos la posibilidad de abordar estos elementos específicos, como mínimo, aprendiendo el manejo de la herramienta de autor DescartesJS, un software libre y multipropósito con el que podrás crear tus propios contenidos interactivos para cualquier materia, respetando los derechos de autor y compartiéndolos en entornos seguros con una licencia Creative-Commons.

Queda abierto, por tanto, el plazo de inscripción gratuita a la III Edición del Curso para el Diseño de objetos interactivos con DescartesJS, una acción formativa que se enmarca en el programa de Educación Abierta desarrollado entre redes docentes de Colombia, México y España, fundamentalmente, aunque contamos con la participación de profesorado de otros países de habla hispana, portuguesa e inglesa. Un curso que tiene como objetivo principal diseñar recursos educativos abiertos en formato de escenas interactivas con la herramienta de autor Descartes JS,  que permitan poner de manifiesto que es posible dar una respuesta positiva y asequible a los retos educativos intrínsecos al paradigma educativo emergente.

Está dirigido a docentes de cualquier etapa educativa, infantil, primaria, educación secundaria obligatoria, bachillerato, formación profesional, enseñanzas de régimen especial y universidad, y de cualquier materia o especialidad, en activo o no, así como a profesionales vinculados a la educación o formación, utilizando una metodología activa, pues desde la primera sesión cada participante comenzará a diseñar y editar su primer recurso interactivo, recibiendo sesiones quincenales por videoconferencia, que serán grabadas y compartidas con todos los participantes y asesorados por docentes de las redes mencionadas.

El curso comienza el próximo día 21 de octubre y finaliza el 3 de marzo de 2023, impartiéndose las sesiones de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al siguiente calendario previsto y contenidos a tratar:

calendario contenido descartesjs

Para cualquier consulta o aclaración, puedes contactar con nosotros en la dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.

 ACCESO AL FORMULARIO DE INSCRIPCIÓN

 

Recursos que utilizaremos:

  1. Descarga el software libre DescartesJS para tu sistema operativo.
  2. Tutorial sobre DescartesJS - Nivel I
  3. Lista en Youtube con vídeos de apoyo
Publicado en Difusión
Etiquetado como
¡Escribe el primer comentario!
Leer más ...
Página 7 de 70

SiteLock

Módulo de Búsqueda

Palabras Clave

Título

Categoría

Etiqueta

Autor

Acceso

Lo último

Lo más leído de lo publicado hace un mes

icono correoCONTACTO

descartes@proyectodescartes.org

Canal Youtube

 Youtube CanalDescartes

Calculadora Descartes

Versión 3.1 con estadística bidimensional

ComparteCódigo para embeber

Utilizamos cookies para mejorar nuestro sitio web y su experiencia al usarlo. Las cookies utilizadas para el funcionamiento esencial de este sitio ya se han establecido. Para saber más sobre las cookies que utilizamos y cómo eliminarlas , consulte nuestra Política de Privacidad.

  Acepto las Cookies de este sitio.
EU Cookie Directive Module Information