Un año más hemos celebrado nuestra Asamblea General Ordinaria en forma presencial, simultaneada con modalidad virtual para aquellos socios y socias que no han podido asistir físicamente, teniendo como punto de encuentro el IES Alhakén II de Córdoba. Por ello, nos desplazamos a la andaluza ciudad milenaria y crisol de civilizaciones desde diversos lugares y puntos geográficos de la península, como Burgos, Lebrija, Baza, Valladolid, Madrid, Santiago de Compostela, Logroño, Santomera, Zaragoza, Santander, Barcelona y Cádiz. Particularmente, para quien suscribe este artículo, y después de tantos años colaborando desde entornos virtuales, ha sido un placer conocer personalmente a nuestra compañera Elena Álvarez y reencontrarme con Paco Rodríguez y Luis Barrios.

No se trataba de una normal asamblea, pues conmemoramos la efemérides del 25º Aniversario del Proyecto Descartes y de la herramienta de autor Descartes, habiendo canalizado con anterioridad algunas acciones como el artículo enlazado, una especial línea de tiempo y la monotemática, para esta ocasión, Revista Digital de la RED Descartes. Así que, tras el desarrollo preceptivo en lo referente a tareas como gestión y organización, memoria y propuesta de actividades, cierre económico y propuesta de presupuestos, fuimos adentrándonos en nuestra historia, alternando con la situación actual en base a una pregunta como eje vertebrador: "¿Cuáles han sido las claves para que hoy, 25 años después, los recursos educativos abiertos creados con la herramienta de autor Descartes sigan siendo objeto de gran aceptación entre los profesionales del mundo de la enseñanza y educación?"

Hemos valorado las nuevas incorporaciones y actualizaciones que ofrecemos en el ingente repositorio de recursos educativos abiertos e interactivos validados en el aula, para todas las modalidades de enseñanza y etapas educativas, desde infantil a universidad, generados con dos potentes herramientas de software libre, constituyendo nuestra humilde aportación altruista a los Objetivos de Desarrollo Sostenible de la UNESCO, especialmente el denominado ODS4, Educación de Calidad: la educación es la base para mejorar nuestra vida y el desarrollo sostenible. Aún así, somos conscientes del importante número de estudiantes y centros que, desgraciadamente, se ven obligados a usar entornos de aprendizaje virtuales y recursos con una baja conectividad, por lo que ponemos a su disposición nuestra e-publicación, desde donde pueden descargarse todos los recursos y utilizarlos en modo local sin navegar por internet. A su vez, consideramos el rendimiento de la Editorial RED Descartes, que amplía constantemente el número de volúmenes en las estanterías de nuestra biblioteca gratuita, ofreciendo, además, el mismo libro en formato PDF con enlaces a los recursos multimedia, con el fin de facilitar el aprendizaje a las personas que disponen de una baja conectividad.  

Queremos mostrar desde aquí nuestro más sincero agradecimiento al equipo directivo del IES Alhakén II, y muy especialmente a D. Antonio Jesús López Olmedo, secretario del mismo, por su cálida acogida y exquisito trato dispensado, así como por facilitar el desarrollo de la asamblea general de RED Descartes, como no puede ser de otra manera por nuestra profesión, en un entorno educativo y académico.

Aprovechando  la estancia en Córdoba, primera ciudad con cuatro declaraciones de la Unesco de Patrimonio de la Humanidad, y con nuestro compañero Pepe Galo como anfitrión, pudimos conocer, en las estribaciones de Sierra Morena, las ermitas y la ciudad califal de Medina Azahara (visita nocturna guiada), el grandioso edificio, con trece siglos de historia, que constituye la Mezquita-Catedral (visitas diurna y nocturna), el  patio de los naranjos y la torre de la catedral que encapsula al alminar árabe pudiendo verse parcialmente en su interior, así como el entorno de la mezquita, puerta del puente, puente romano y noria de la Albolafia. Sin embargo, la emoción te asalta cuando paseas por la judería y te encuentras frente a Maimónides o Al-Gafequi, continúas hacia la sinagoga, la muralla de la Medina con la puerta de Almodóvar y, nuevamente, te detienes frente a las estatuas de Séneca y Averroes, siendo un buen momento para recordar y reflexionar sobre esta ciudad que un día, como capital de Al Ándalus, concentró el conocimiento de la humanidad con estos grandes sabios, filósofos y científicos, y nos viene a la memoria que la obra los Elementos de Euclides (ver página 69 en este enlace) llegó a la península ibérica directamente a la Biblioteca de Alhakén II en Medina Azahara, ciudad natal de Abulcasis, «padre de la cirugía moderna», quien siguió los pasos del gran Euclides para recopilar todos los conocimientos sobre medicina en su época.

Para conocer o profundizar en el concepto de proporción cordobesa en las construcciones árabes de la ciudad, recomendamos los siguientes recursos interactivos:

• La proporción cordobesa o humana
• Rectángulos cordobeses y áureos en el frontal del Mihrab de la Mezquita de Córdoba
• Triángulo, rectángulo y diamante cordobés. Tesela.

También tuvimos la oportunidad de visitar el monumento a los enamorados en memoria del amor entre el poeta Ibn Zaydun y la poeta y princesa Wallada, el barrio de San Basilio, Alcázar de los Reyes Cristianos y Baños Califales, el casco histórico de Córdoba (la Medina y la Axerquía) y parcialmente la ruta de las Iglesias Fernandinas (construidas por Fernando III el Santo), la plaza y Posada del Potro y, como no podía ser de otra manera, la pintura cordobesa en el Museo de Julio Romero de Torres.

Obviamente, pudimos degustar la variada y extraordinaria gastronomía cordobesa, destacando por desconocimiento de la mayoría de asistentes el plato conocido como mazamorra, que recomendamos probar. A su vez, en uno de los establecimientos recibimos con mucho cariño, y mostramos desde aquí nuestro agradecimiento, un plato conmemorativo que compartimos:

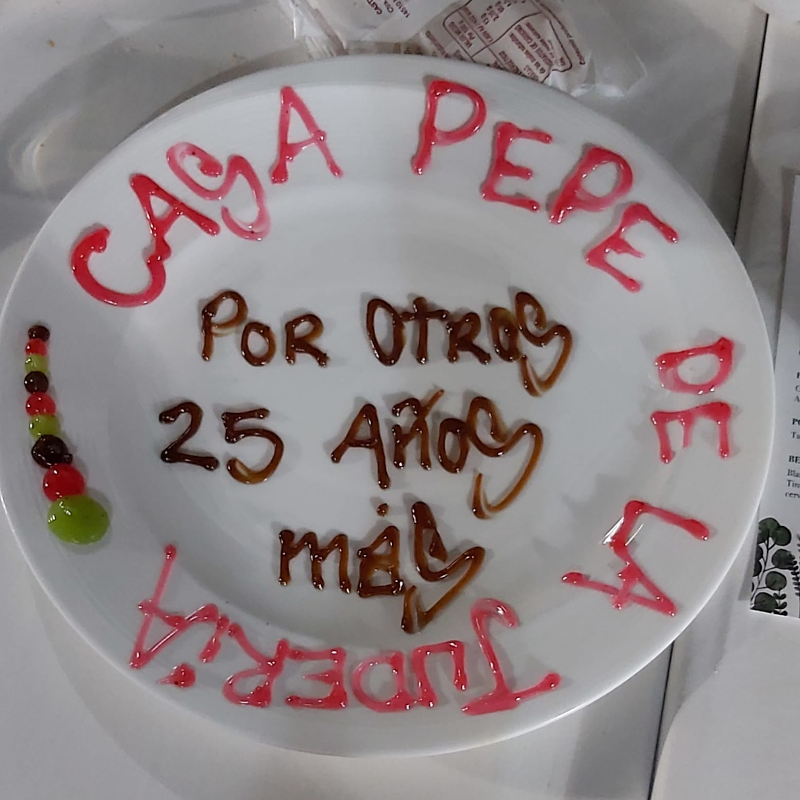
También compartimos el vídeo editado por nuestra compañera Solín Ruiz con las aportaciones de todos los participantes desde nuestro grupo de WhatsApp, donde se recogen momentos de la reunión, visitas a los distintos monumentos del patrimonio cordobés e instantes de ocio y divertimento:

La concha del Nautilus, un prototipo de belleza natural ampliamente divulgado, es un icono que habitualmente se utiliza para mostrar cómo la Naturaleza hace matemáticas. Pero el canon aúreo en el que insistente y cansinamente se le encuadra es erróneo. ¡El Nautilus es cordobés!, así lo demostramos en nuestro modelo uniforme (Galo J.R., Cabezudo A. y Fernández I., 2016) —modelo donde se considera que el crecimiento que acontece en todas las etapas vitales es siempre el mismo—. No obstante, como es habitual en todo ser vivo, la ontogenia de este animal presenta alometrías que quedan reflejadas en su concha y que pedían ser matemáticamente desentrañadas. Esto es lo que se detalla en el "Modelo ontogénico matemático del Nautilus" que aquí les presento.

Le invito a conocer este modelo e inicialmente, para situarle, le mostraré el cuaderno de bitácora de la investigación (que sintetiza lo publicado en artículos anteriores en este blog de RED Descartes) y posteriormente le detallaré el modelo matemático ontogénico en sí.

Queda cubierta una etapa ardua, y simultáneamente muy gratificante, en la que el Nautilus ha ido progresivamente activando mis neuronas hasta lograr descodificar y comprender el porqué matemático del rastro vital que va esculpiendo a medida que conforma su concha. Pero todo nuevo conocimiento más que actuar como cierre lo que suele proceder es como catalizador de nuevos objetivos y, por ello, mis siguientes pasos se centrarán en atisbar qué acontece fuera del la sección sagital bidimensional del Nautilus analizada y descrita en este artículo. La concha del Nautilus es tridimensional y, de nuevo, mi oído y el resto de sentidos incluido el sentido matemático, quedan prestos a desentrañar los susurros de mi paisano cordobés. Les emplazo a que más adelante lean mis avances al respecto y a que compartan sus opiniones y observaciones...  tengan paciencia. Hasta pronto.

Cuaderno de bitácora  

En la siguiente presentación tiene reflejado, sintéticamente, el camino seguido en esta investigación. Se incluyen hiperenlaces a artículos en los que puede profundizar sobre algún aspecto concreto.

Cuaderno de bitácora (puede controlar este recurso con el menú ፧ ubicado en la parte inferior)  o verlo en este pdf: 

Modelo ontogénico matemático del Nautilus

A partir del análisis previo he llegado al Modelo ontogénico del Nautilus que se desglosa en la siguiente presentación.

Modelo ontogénico matemático del Nautilus. 

Todo lo anterior puede observarse en el siguiente recurso interactivo, que por defecto se presenta como una animación, pero puede pasar a modo manual sin más que pulsar el botón inferior izquierda, que está etiquetado con la imagen de una mano, y usar el control "paso".

Recurso interactivo donde se describe el modelo ontogénico matemático del Nautilus. Acceso a ventana completa y a las indicaciones.

Este modelo ontogénico puede observarse en la siguiente imagen animada. Al no tener datos sobre la temporalización real del crecimiento del Nautilus se ha asignado el mismo tiempo a cada septo.

Imagen animada del modelo ontogénico matemático del Nautilus

Bibliografía 

Galo J.R., Cabezudo A. y Fernández I.(2016 a) : Sobre la forma y crecimiento cordobés del Nautilus Pompilius. Epsilon, 2016, Vol. 33 (3), nº 94.

Greenwald L., Ward P.D. (2010) Buoyancy in Nautilus. In: Saunders W.B., Landman N.H. (eds) Nautilus. Topics in Geobiology, vol 6. Springer, Dordrecht.

Landman, N. H., Arnold, J. M. and Mutvei, H. 1989: Description of the embryonic shell of Nautilus belauensis. American Museum Novitates, no. 2960, p. 1–16.

Mutvei, H. and Doguzhaeva, L. 1997: Shell ultrastructure and ontogenetic growth in Nautilus pompilius L. (Mollusca: Cephalopoda). Palaeontographica Abteilung A Palaeozoologie–Stratigraphie, vol. 246, p. 33–52.

Tanabe K. & Uchiyama, K.  1997. Development of the Embryonic Shell Structure in Nautilus. The Veliger 40(3): 203-215.

Thompson, D’A. W., (1917). On growth and Form. Cam. Univ. Press.

Ward, P. (1979). Cameral liquid in Nautilus and ammonites. Paleobiology, 5(1), pp. 40-49.

Ward, P., Greenwald, L., & Magnier, Y. (1981). The chamber formation cycle in Nautilus macromphalus. Paleobiology, 7(4), 481-493. doi:10.1017/S0094837300025537

 
Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional